因果関係の推定 〜Pythonによる傾向スコアマッチングとIPW〜

　　
中学生のときに目がよく合うと感じた人がいたら、それは自分に絶大な好意を持っているからだと思い込んでいましたよね。しかし、現実は思い出のままでした。それは、「よく目が合う」ことと「好意を持つ」ことは相関しているかもしれませんが、因果の関係とまでは言えないからです。自分の隣の人をガン見していたついでに自分を見ていただけかもしれません。まさに想いの交絡です。

正常な話に戻すと、因果を見つけることは大事です。因果がわかると次に何が起きるかを間違えることなく予測できます。まさに、預言者です。相関と因果は違うというのは頭ではわかっています。しかし、相関の壁を飛び越えていける人はごく僅かです。そこで今回は、因果関係を定量的に測定する統計的因果推定をPythonを使って行います。先人の方々が同じような内容をすでに書いていますが、傾向スコアマッチングとIPWの結果が異なっているという結論が多かったので、IPWにおいて上下限を指定し、傾向スコアマッチングの結果と遜色ないようにしました。

今回のコードはこちらのGitHubに置いてあります。

統計的因果推定をざっくり理解

相関と因果は似て非なるものというのは、すでに万人が知っています。ただ、相関の求めやすさに比して、因果の関係性を調べるのは困難です。そのため、世の分析では簡単に求められる相関止まりのものが多いです。

因果を求めることが難しいのは、データの理解、分析の設定、アルゴリズムの理解などが必要な点であり、今や１行で求められる相関係数と比べると面倒だと感じる人も多いでしょう。逆に言うと、相関係数だけの分析は本来加味しなければいけない情報を省いているとも言えます。絶対的に正しい指標はないので、両方を知っておくことは大事です。

統計的因果推定における出演者は、『被説明変数』、『割り当て変数』、『共変量』の３役です。この3役が揃ってこそ因果応報な感情のもつれ合うドラマが繰り広げられるわけです。それぞれの変数の意味は次の通りです。被説明変数は目的となる変数で、この変数で良し悪しを判断します。割り当て変数は、施策の対象者か否かといった2つのグループに分ける変数であり、この割り当てによって被説明変数に差が生まれているかを見ます。また、被説明変数と割り当て変数の両方に影響を与える変数が共変量です。

これら３つの変数の関係性は以下の通りであり、被説明変数は、割り当て変数と共変量から影響を受け、割り当て変数は共変量から影響を受けます。ただこの状態だと、問題があります。それは、\(z\)が良いことをしたときに\(y\)が上機嫌でも、\(z\)の行為によってそうなったのか、\(\mathrm x\)の影響なのかがわからないことです。\(\mathrm x\)に触発されて\(z\)が行為をしたと\(y\)が感じたら、\(\mathrm x\)の好感度が上がってしまいますね。

問題の本質

今回解決したい問題は、『何かしらの手を加えた２つの集団（割り当て）において、見たい変数（被説明変数）に本当に違いがあるのかを知りたい』です。例えば、新人研修をした人としていない人で１年後の年収に違いがあるのかを求めたいとします。その際によく行うのは、新人研修の有無で2つのグループに分け、平均や中央値をグループ間で比較します。この方法によって２つのグループの差がわかり、新人研修を行ったグループの年収の平均値の方が高ければ、新人研修は効果があるということになります。

しかしながら、この平均値や中央値が２つのグループの真の差なのかというのが、今回の問題提議です。例えばこの新人研修が、知る人ぞ知る人しか申し込めなかったとしたら、参加者は情報収集能力が高い人たちの集合です。もし、年収と入社前のツイッターのフォロワー数の関係が強いという傾向があった場合、新人研修のおかげで１年後の年収が上がったというよりは、フォロワー数が多い人の年収が上がりやすく、その人達が新人研修に参加したグループに多かったということになります。つまり、新人研修が年収を上げるとは言えないのです。

何かしらにより２つのグループに分けて（先程の例では、新人研修をしたか否か）、そのグループ間での被説明変数の差を見るときには、グループ間で共変量（先程の例では、フォロワー数）の偏りがないかを確認する必要があります。

強く無視できる割り当て

　

統計的因果推定がなぜ必要かというと、単純なグループ間での被説明明変数の比較だと、共変量の影響を含んだ割り当ての効果をみてしまうという問題があるからでした。逆に言うと、共変量の偏りを修正すればよいわけです。

共変量に偏りがあることが問題なので、共変量に偏りが生まれないようにするため、グループをランダムに分けていれば、正しい効果を測定できます。先程の例では、新人研修をしたグループとしていないグループが自然とできており、共変量にグループ間での偏りがなければ、グループ間での年収の差が新人研修の効果を表します。世の中のグループ間での平均の比較は、ランダム割り当てたことを前提としているわけです。

しかしながら、現実世界では、割り当てには共変量の偏りが起きてしまうものです。それならば現実をそのまま受け入れて、割り当てはそのままで、同等な共変量の値で比較することによって効果を測定します。ツイッターのフォロワー数が同等の人たちの中で、新人研修の有無での年収の差を見れば、フォロワー数が影響しない新人研修による年収の差がわかります。つまり、共変量を同等にすれば、割り当て変数による被説明変数の効果がわかります。

共変量が同等であれば、処置群（施策を行った群）と対照群（施策を行わなかった群）という情報だけでは被説明変数を予測できなくなります。これは、「割り当てが共変量のみに依存し、被説明変数には依存しない」ということであり、強く無視できる割り当てと呼ばれます。数式で表すと以下になります。

\(\displaystyle (y_1, y_0) \ \ \!\!\!\perp z|\mathrm x\)

この式は条件付き確率で表すと以下のようになります。共変量を条件づけたときの割り当て確率は、被説明変数とは独立である場合に、強く無視できる割り当てとなます。そして、その割り当てのグループ間での被説明変数の差によって、割り当ての効果を測定できます。

\(\displaystyle p(z|y_1, y_0, \mathrm x) = p(z|\mathrm x)\)

傾向スコア

共変量を条件つけて、同等な共変量同士で割り当て間での比較をすることで、割り当てによる被説明変数の効果を測定できます。上の例の場合では、共変量はツイッターのフォロワー数のみという１変数だけだったので、同等な共変量同士による比較は行いやすかったです。しかし、共変量が複数になると同等なものを見つけるのは難しくなります。

そこで、共変量を１変数に集約することで、同等なものを見つけやすくします。共変量を入力、割り当てを出力とする確率推定モデルを作り、推定された確率で条件付を行うことで、割り当ての効果を測定できるようにします。このとき、確率推定モデルにより推定された確率を傾向スコアと呼びます。因みに、確率推定モデルとしてロジスティック回帰がよく使われます。

傾向スコアによる統計的因果推定を実践

それでは、統計的因果推定をPythonを使って実行します。順序としては、データを取得し、データの中身を確認し、傾向スコアを求め、因果推定をします。

データの取得

今回使用するデータは、NSWD Dataです。これは、労働市場に参加できていない人に対する、カウンセリングと9〜18ヶ月の短期的な就労体験の有無、その後の年収、その人の属性が含まれたデータです。このデータは、短期的な就労体験を割り当て変数、被説明変数をその後の年収とした因果推定の題材としてよく使われます。

このデータの良いところは、ランダムな割り当てと恣意的な割り当てのデータが用意されていることです。この２つのデータを使って統計的因果推定の結果を比較することで、統計的因果推定のアルゴリズムの良し悪しがわかります。恣意的に割り当てを含んだデータに対する推定の結果が、ランダムな割り当てのデータに対する結果に近づけば良いアルゴリズムということです。

それでは、データを取得します。まずは必要なモジュールをインポートします。

モジュールのインポート

from pathlib import Path
from dfply import *
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import NearestNeighbors
import statsmodels.api as sm
import seaborn as sns
import matplotlib.pyplot as plt

次に、NSWDデータを取得します。pandasを使えば簡単に取得できます。

データの取得

cps1_data = pd.read_stata('https://users.nber.org/~rdehejia/data/cps_controls.dta')
nswdw_data = pd.read_stata('https://users.nber.org/~rdehejia/data/nsw_dw.dta')

データの中身は以下のとおりです。「treat」が短期的な就労体験の有無を表す割り当て変数であり、re78が被説明変数であり、就労体験後の年収です。

比較データの作成

因果推定のアルゴリズムを評価するために、ランダムに割り当てた理想的なデータと比較用のデータを作成します。ランダムに割り当てたデータの就労体験を経験した群に、異なる調査用のデータを就労体験が未経験として結合します。結合したデータは就労体験とは関係がないので、この結合によって割り当てのグループ間で共変量の偏りが生まれるようにしています。

cps1_nsw_data = nswdw_data >> filter_by(
    X.treat == 1
) >> bind_rows(
    cps1_data
)
cps1_nsw_data.reset_index(inplace=True, drop=True)

データの理解

データのグラフ化

データを取得したので、データの中身を確認します。何を見たいかというと、割り当てグループ間での被説明変数と共変量の関係性です。ここでは、共変量を連続変数とカテゴリ変数に分けてグラフ化しています。２つのデータでの違いを見たいので、このグラフ化プログラムを関数化しておきます。ポイントは共変量のそれぞれの変数と被説明変数を散布図で表すために、seabornのFacetGridとcatplotを使えるようにデータをstack関数で縦長に変換していることです。

def plot_treat_in_target(target_data, y_name, z_name, category_names, numeric_names, n_threshold=1000, image_base_file_path=None):
    
    target_data1 = target_data.loc[target_data[z_name] == 1, :].copy()
    target_data0 = target_data.loc[target_data[z_name] == 0, :].copy()
    if len(target_data1) > n_threshold:
        target_data1 = target_data1 >> sample(n_threshold)
    if len(target_data0) > n_threshold:
        target_data0 = target_data0 >> sample(n_threshold)
        
    target_data = target_data1 >> bind_rows(target_data0)
    

    # 被説明変数と介入変数のグラフ化
    sns.swarmplot(
        x=z_name, 
        y=y_name, 
        data=target_data
    )
    
    if image_base_file_path:
        plt.tight_layout()
        plt.savefig(image_base_file_path.__str__()+'_y_z.png')
     
    # 被説明変数と連続変数のグラフ化
    if len(numeric_names) > 0:

        plot_data = target_data >> select(numeric_names + [y_name, z_name])
        plot_data = plot_data.set_index([y_name, z_name])
        plot_data = plot_data.stack()
        plot_data = plot_data.reset_index(drop=False)
        plot_data.columns = [y_name, z_name, 'colname', 'value']


        kws = {'scatter_kws':{'alpha':'0.2'}}
        g = sns.FacetGrid(plot_data, col='colname', hue=z_name, col_wrap=4, sharex=False, height=5)
        g.map(sns.regplot, 'value', y_name, **kws)
        g.add_legend()
        g.set_axis_labels("", "")
        g.set_titles(size=15)
        
        if image_base_file_path:
            
            plt.tight_layout()
            plt.savefig(image_base_file_path.__str__()+'_y_z_numeric.png')

    # 被説明変数とカテゴリ変数のグラフ化
    if len(category_names) > 0:
        plot_data = target_data >> select(category_names + [y_name, z_name])
        plot_data = plot_data.set_index([y_name, z_name])
        plot_data = plot_data.stack()
        plot_data = plot_data.reset_index(drop=False)
        plot_data.columns = [y_name, z_name, 'colname', 'value']

        g = sns.catplot(
            x=z_name,
            y=y_name,
            hue='value',
            col='colname',
            kind='violin',
            data=plot_data,  
            col_wrap=4, 
            sharex=False,
            height=5,
            dodge=True
        )
        g.add_legend()
        g.set_titles(size=15)
        
        if image_base_file_path:
            plt.tight_layout()
            plt.savefig(image_base_file_path.__str__()+'_y_z_category.png')
        

この関数を使って、被説明変数と割り当て変数、共変量のそれぞれの変数との関係性を見ていきます。

y_name = 're78'
z_name = 'treat'
category_names = ['black', 'married', 'nodegree']
numeric_names = ['age', 'education', 're74', 're75']


plot_treat_in_target(
    target_data=nswdw_data.copy(),
    y_name=y_name,
    z_name=z_name,
    category_names = category_names,
    numeric_names = numeric_names,
    n_threshold=1000,
    image_base_file_path=image_dir_path.joinpath('nsw')
)

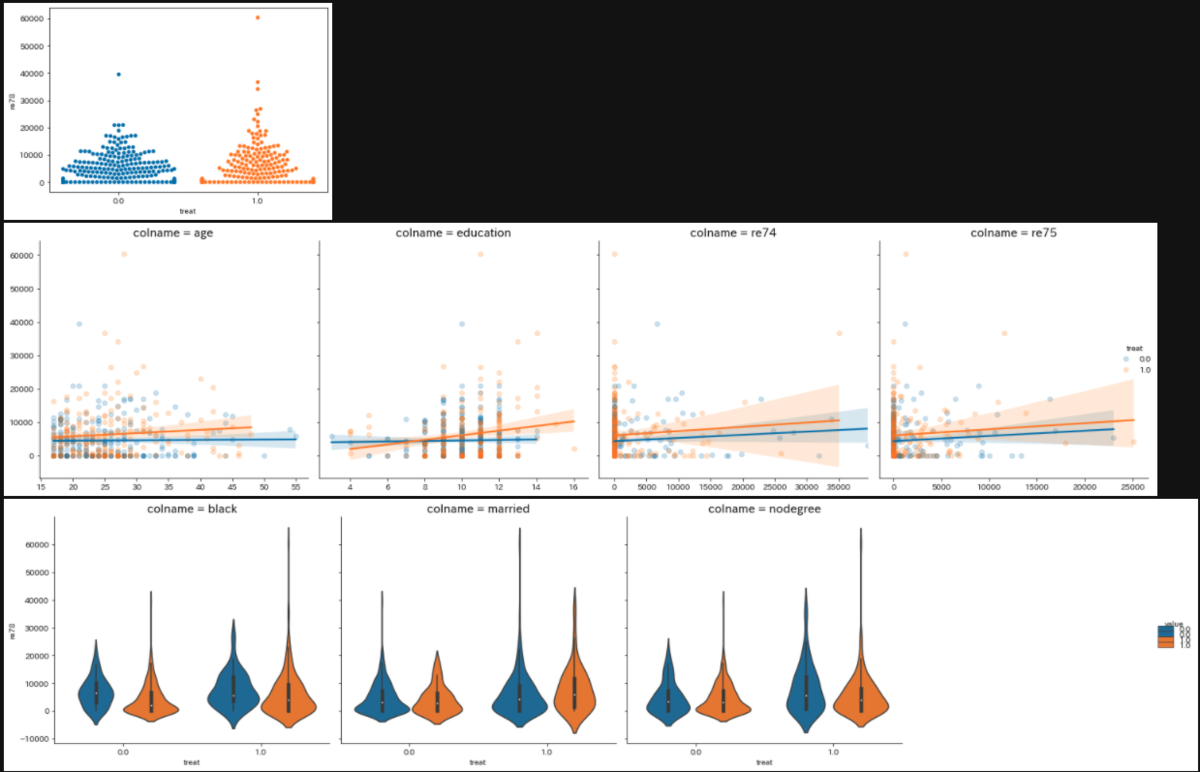
ランダムに割り当てただけあって、割り当て変数「treat」と被説明変数「re78」の散布図では同じような分布になっています。共変量のそれぞれの変数で見ても、若干education変数においてre78変数と相関してそうといったぐらいですね。

それでは、比較する恣意的データでの関係性を見てみます。

plot_treat_in_target(
    target_data=cps1_nsw_data.copy(),
    y_name=y_name,
    z_name=z_name,
    category_names = category_names,
    numeric_names = numeric_names,
    n_threshold=1000,
    image_base_file_path=image_dir_path.joinpath('cps1')
)

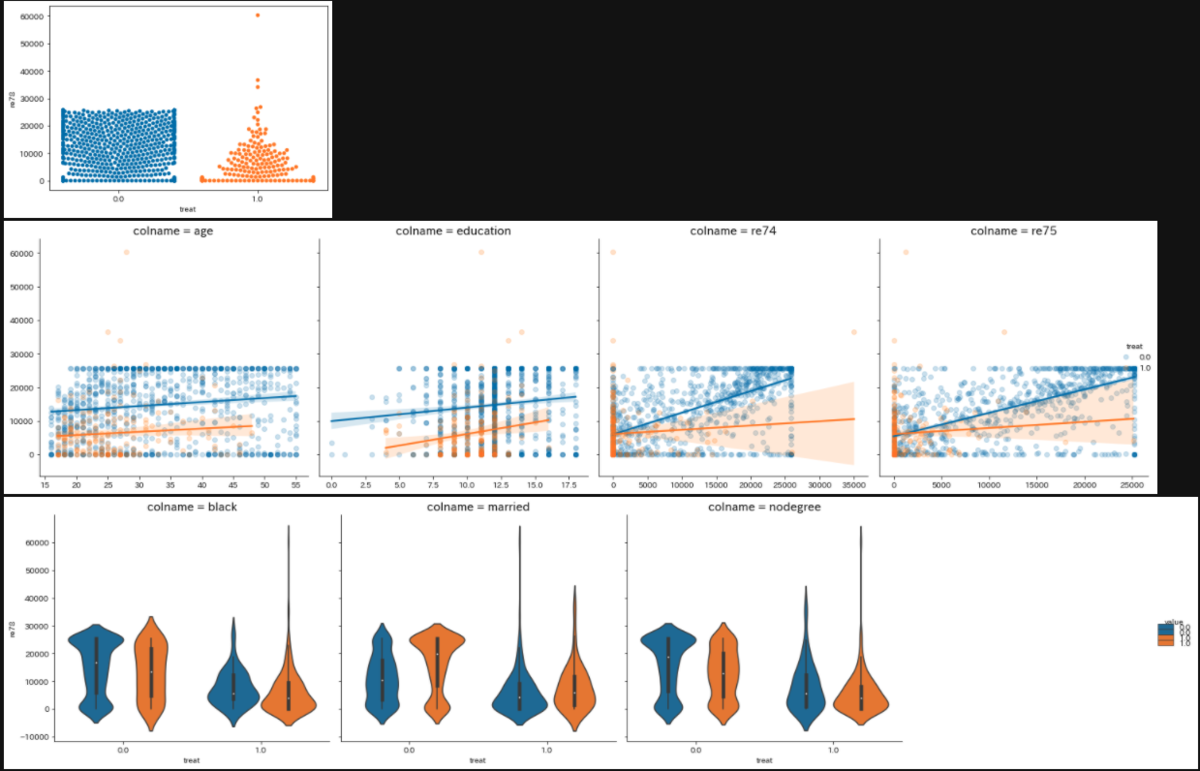
treat変数とre78変数の散布図を見ると、明らかに対照群の方が高収入が多いですし、re74、re75変数とre78変数の散布図では、対照群の方が相関しています。married変数（結婚しているか否か）においても、対照群と処置群では分布が大きく異なっています。このまま、treatグループ間でのre78の代表値の比較をすると、treatの差というよりは、re74、re75などのもともとの属性の差とも言えてしまいます。

代表値による比較

グラフ化してみた結果、処置群と対照群では共変量の分布に違いがあることがわかりました。このまま平均値と中央値を算出してみたらどうなるかを見てみます。

result_nsw = nswdw_data >> group_by(X.treat) >> summarise(
    n=X.treat.count(),
    re78_mean=X.re78.mean().round().astype(int),
    re78_median=X.re78.median().round().astype(int),
    re78_std=X.re78.std().round().astype(int)
) >> mutate(treat=X.treat.astype(int))

result_cps = cps1_nsw_data >> group_by(X.treat) >> summarise(
    n=X.treat.count(),
    re78_mean=X.re78.mean().round().astype(int),
    re78_median=X.re78.median().round().astype(int),
    re78_std=X.re78.std().round().astype(int)
) >> mutate(treat=X.treat.astype(int))

下の図が代表値計算の結果です。ランダム割り当て、恣意的割り当ての対照群の平均値と中央値は大きく異なっていることがわかります。またどちらのデータにおいても、平均値と中央値には差があり、標準偏差が大きいです。この代表値をもとに2群の差を見てしまうと、誤った結果を得そうです。

ランダム割り当てデータ

恣意的割り当てデータ

傾向スコアの算出

データのグラフ化により、恣意的な割り当てデータにおいて、グループ間での共変量に偏りがあることがわかりました。なので、統計的因果推定が必要です。今回は、傾向スコアを使った統計的因果推定を行うので、まずは傾向スコアを求めます。

共変量を入力、割り当て変数を出力とするロジスティック回帰モデルを作り、割り当ての推定確率を傾向スコアとします。

def make_ps_score_data(X_data, z_data):

    model = LogisticRegression(
        penalty='l1', 
        max_iter=10000,
        solver='liblinear',
        random_state=42
    )
    model.fit(X_data, z_data)

    ps_score_data = pd.DataFrame({
        'z': z_data, 
        'ps_score': model.predict_proba(X_data)[:, 1]
    })
    return ps_score_data


z_name = 'treat'
X_names = list(filter(lambda x: x != y_name and x != z_name, target_data.columns))

plt.figure(figsize=(10, 6))
ps_score_data_nsw = make_ps_score_data(
    X_data=nswdw_data >> select(X_names),
    z_data=nswdw_data[z_name]
)
sns.distplot(ps_score_data_nsw.loc[ps_score_data_nsw['z'] == 1, 'ps_score'], label='処置群', bins=50)
sns.distplot(ps_score_data_nsw.loc[ps_score_data_nsw['z'] == 0, 'ps_score'], label='対照群', bins=50)
plt.legend()
plt.xlabel('傾向スコア')
plt.xlim(0, 1)
plt.tight_layout()
plt.savefig(image_dir_path.joinpath('ps_score_distibution_nsw.png'))


plt.figure(figsize=(10, 6))
ps_score_data_cps = make_ps_score_data(
    X_data=cps1_nsw_data >> select(X_names),
    z_data=cps1_nsw_data[z_name]
)
sns.distplot(ps_score_data_cps.loc[ps_score_data_cps['z'] == 1, 'ps_score'], label='処置群', bins=50)
sns.distplot(ps_score_data_cps.loc[ps_score_data_cps['z'] == 0, 'ps_score'], label='対照群', bins=50)
plt.legend()
plt.xlabel('傾向スコア')
plt.xlim(0, 1)
plt.tight_layout()
plt.savefig(image_dir_path.joinpath('ps_score_distibution_cps.png'))

上記の結果は以下のとおりです。ランダム割り当てのデータは傾向スコアがバランス良く分布していますが、恣意的割り当てのデータは、対照群の傾向スコアが0付近に偏っています。0付近の傾向スコアが多いことは注意が必要ですね。

傾向スコアマッチング

傾向スコアを求めたところで一度これまでを振り返ると、同等な共変量同士を比較すれば、共変量に依存しない割り当ての効果を検証できるので、因果関係があるかわかるのでしたね。しかしながら、共変量が複数変数の場合は同等な共変量のペアを見つけるのは困難なので、1変量に集約してしまえということで傾向スコアを求めました。なので、割り当て間で同等な傾向スコア同士の被説明変数を比較して効果を測定します。これが傾向スコアマッチングです。

傾向スコアマッチングの実行

傾向スコアマッチングのプログラムは以下のように作ってみました。ポイントは、最近傍法で割り当て間での傾向スコアのマッチングをどちらかのデータが無くなるまで行っているところです。それ以外のところは、dfplyモジュールの扱いに慣れていれば直感的かなと思います。

def get_matched_propensity_score(target_data, y_name, z_name, x_names, threshold=0.2):
    
    
    ps_score_data = make_ps_score_data(
        X_data = target_data >> select(x_names),
        z_data = target_data[z_name]
    )
    ps_score_data['index_all'] = target_data.index
    ps_score_data['y'] = target_data[y_name]
    

    treatment_data = ps_score_data >> filter_by(X.z == 1) >> rename(
        index_treatment=X.index_all
    )
    treatment_data.reset_index(inplace=True, drop=True)
    control_data = ps_score_data >> filter_by(X.z == 0) >> rename(
        index_control=X.index_all
    )
    control_data.reset_index(inplace=True, drop=True)


    match_index_data = pd.DataFrame()
    treatment_data_tmp = treatment_data.copy()
    control_data_tmp = control_data.copy()


    while len(treatment_data_tmp) > 0 and len(control_data_tmp) > 0:

        neigh = NearestNeighbors(n_neighbors=1, algorithm='ball_tree')
        neigh.fit(control_data_tmp['ps_score'].values.reshape(-1, 1))
        distances, indices = neigh.kneighbors(treatment_data_tmp['ps_score'].values.reshape(-1, 1))

        distance_data = pd.DataFrame({
            'distance': distances.reshape(-1), 
            'index_treatment': treatment_data_tmp['index_treatment'].values,
            'index_control' : control_data_tmp['index_control'][indices.reshape(-1)]
        }) >> filter_by(X.distance <= threshold) >> arrange(X.distance) >> distinct(X.index_control)

        if len(distance_data) == 0:
            break

        match_index_data = match_index_data >> bind_rows(
            distance_data >> select(X.index_treatment, X.index_control, X.distance)
        )

        treatment_data_tmp = treatment_data_tmp >> anti_join(distance_data, by='index_treatment')
        control_data_tmp = control_data_tmp >> anti_join(distance_data, by='index_control')

        treatment_data_tmp.reset_index(inplace=True, drop=True)
        control_data_tmp.reset_index(inplace=True, drop=True)

        
    match_index_data = match_index_data >> arrange(X.index_treatment)
    match_index_data.reset_index(inplace=True, drop=True)

    matched_ps_data = match_index_data >> left_join(
        ps_score_data >> rename(
            y_treatment=X.y,
            ps_score_treatment=X.ps_score,
            index_treatment=X.index_all
        ) >> select(
            X.index_treatment, X.y_treatment, X.ps_score_treatment
        ), by='index_treatment' 
    ) >> left_join(
        ps_score_data >> rename(
            y_control=X.y,
            ps_score_control=X.ps_score,
            index_control=X.index_all
        ) >> select(
            X.index_control, X.y_control, X.ps_score_control
        ), by='index_control' 
    ) >> mutate(y_diff=X.y_treatment-X.y_control)
    
    
    target_data_lr = matched_ps_data >> select(X.y_treatment) >> mutate(z=1) >> rename(
        y=X.y_treatment
    ) >> bind_rows(
        matched_ps_data >> select(X.y_control) >> mutate(z=0) >> rename(
            y=X.y_control
        )
    )
    X_data = target_data_lr >> select('z')
    X_data = sm.add_constant(X_data)
    
    model = sm.OLS(target_data_lr['y'], X_data)

    results = model.fit()
    results = results.summary()
    
    return results, matched_ps_data

それでは、上記の関数を使って両方のデータにおける傾向スコアマッチングの結果を見てみましょう。

target_data = nswdw_data >> select(~X.data_id)

y_name = 're78'
z_name = 'treat'
x_names = list(filter(lambda x: x != y_name and x != z_name, target_data.columns))

results, matched_ps_data = get_matched_propensity_score(
    target_data=target_data.copy(),
    y_name=y_name,
    z_name=z_name,
    x_names=x_names,
    threshold=0.2
)

results

ランダム割り当てのデータにおいて、就労体験の効果は1696ドルになりました。p値は1.6%であり、有意水準が5%ならば棄却できますが、1%ならば棄却できません。1.6%なので大目にみるとして、95%の信頼区間では336~3055なので、プラスの効果がある、つまり、就労体験は効果があったと言えます。

　
恣意的なデータに対して効果を測定できるか試してみます。

target_data = nswdw_data >> select(~X.data_id)

y_name = 're78'
z_name = 'treat'
x_names = list(filter(lambda x: x != y_name and x != z_name, target_data.columns))

results, matched_ps_data = get_matched_propensity_score(
    target_data=target_data.copy(),
    y_name=y_name,
    z_name=z_name,
    x_names=x_names,
    threshold=0.2
)

results

恣意的な割り当てのデータにおいて、就労体験の効果は1722ドルになりました。先程と比べると若干効果を上に見積もっていますが、極端な割り当ての違いを考えると大健闘ですね。

共変量のバランス

傾向マッチングによって傾向スコアを使った統計的因果推定ができました。ところで、なぜこのような回りくどいやり方をしなければいけなかったかというと、割り当てグループ間で共変量の偏りがあるからでした。ということは、傾向スコアマッチングによってできた傾向スコアのペアを新たな割り当てグループとしたら、共変量の偏りが減少しているはずです。

実際に共変量のバランスが良くなっているかを見てみます。こちらのコードは長くなったので、GitHubでご覧ください。

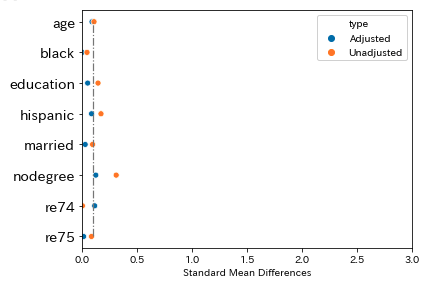
ランダムな割り当てデータでの共変量のバランス
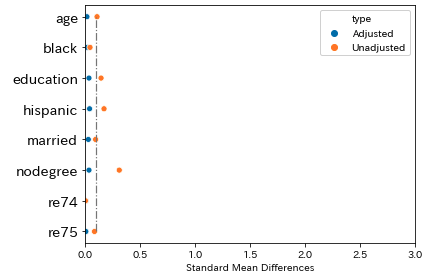
下記の図では、Adjustedが傾向スコアマッチング後の割り当てデータによるグループ間での効果量であり、Unadjustedが元データのグループ間での効果量です。傾向スコアマッチングにより、re74変数以外はグループ間での差が小さくなっており、偏りが減少していることがわかります。

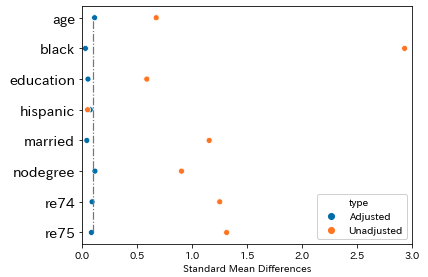
恣意的な割り当てデータでの共変量のバランス
恣意的なデータにおいては、元データの割り当てグループ間での差は明らかに大きいです。そして、傾向スコアマッチングにより、どの変数においても偏りを減少することができています。

IPW

傾向スコアを使った統計的因果推定の方法は、マッチング以外にもあります。それは、逆確率重み付き推定（Inverse Probability Weighting ; IPW）です。傾向スコアは、処置群だと高くなりがちで、対照群だと低くなりがちです。そこで、傾向スコアの逆数をかけたものを重みとして、割り当て間での傾向スコアの分布を整えます。

IPWの実行

IPWを行うために関数を作ります。ポイントは、傾向スコアの逆数の重みを作り、その重みを使って重み付き線形回帰を行っているところです。更に、恣意的割り当てデータで求めた傾向スコアは、０付近に多く集まっていることがわかっています。IPWは傾向スコアの逆数を重みとするため、０に近づけば近づくほど重みが極大になり、一部のデータの影響が過度に強くなります。なので、傾向スコアに下限/上限を指定して、ノイズを削減してます。

def get_ipw(target_data, y_name, z_name, x_names, ps_score_min=0.1, ps_score_max=0.9):
    
    target_data['index_all'] = target_data.index

    ps_score_data = make_ps_score_data(
        X_data = target_data >> select(x_names),
        z_data = target_data[z_name]
    )
    ps_score_data['index_all'] = target_data['index_all']

    ps_score_data = ps_score_data >> filter_by(
        X.ps_score <= ps_score_max, X.ps_score >= ps_score_min
    )
    
    ps_score_data = ps_score_data >> mutate(
        iestep1=(X.z/X.ps_score)*(len(ps_score_data)/ps_score_data['z'].sum()),
        iestep0=((1-X.z)/(1-X.ps_score))*(len(ps_score_data)/(len(ps_score_data)-ps_score_data['z'].sum()))
    ) >> mutate(
        w=X.iestep1+X.iestep0
    )
    
    ipw_data = target_data >> select(
        ['index_all', y_name] + x_names
    ) >> inner_join(
        ps_score_data, by='index_all'
    )
    ipw_data.reset_index(inplace=True, drop=True)
    
    
    y_data = ipw_data[y_name].values
    z_data = ipw_data >> select(X.z) 
    z_data = sm.add_constant(z_data)

    model = sm.WLS(y_data, z_data, weights=ipw_data['w'].values)
    results = model.fit()
    results = results.summary()

    return results, ipw_data

それでは、ランダム割り当てデータに対してIPWを行ってみます。

results, ipw_data = get_ipw(
    target_data=nswdw_data.copy(),
    y_name=y_name,
    z_name=z_name,
    x_names=x_names,
    ps_score_max=0.9,
    ps_score_min=0.1
)
results

推定した効果は1617ドルで、95%信頼区間を見てもプラスの効果になっていることがわかります。

次に恣意的なデータの方で実行します。

results, ipw_data = get_ipw(
    target_data=cps1_nsw_data.copy(),
    y_name=y_name,
    z_name=z_name,
    x_names=x_names,
    ps_score_max=0.9,
    ps_score_min=0.1
)
results

推定した効果は1548ドルであり、傾向スコアマッチング同等のランダム割り当てでの結果に近いものとなりました。p値は若干高いですが（5%以内には収まっています）、95%信頼区間ではプラスなので、やはり短期的な職務体験は効果があることがわかります。

共変量のバランス

傾向スコアマッチングのときと同じように共変量のバランスが良くなったかを確認します。このときのコードはGitHubを御覧ください。

ランダム割り当てデータでの共変量のバランス
もともと割り当て間の差は大きくないですが、IPWによって差がより小さくなっていることがわかります。

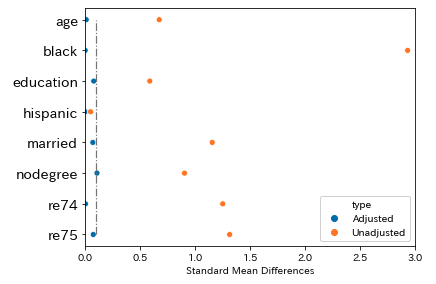
恣意的な割り当てデータでの共変量のバランス
共変量のどの変数でも基準値とした0.1を下回っています。うまくバランシングできています。

終わりに

今回は、傾向スコアを使った統計的因果推定として、傾向スコアマッチングとIPWを実践しました。傾向スコアマッチングとIPWの両方において、ノイズの影響を除いた因果推定ができました。この結果を得られたのは、下記の本でイメージが深まったからだと思います。

効果検証入門〜正しい比較のための因果推論/計量経済学の基礎

参考文献

以下の文献を参考にさせていただきました。ありがとうございます。

• 「効果検証入門 3章 傾向スコアを用いた分析」+αをPythonでやってみる - Qiita
• Pythonで傾向スコア(Propensity score)マッチングとIPWを実装してみた - Np-Urのデータ分析教室
• Covariate Balancing Propensity Scoreを用いた，スクイズ作戦の有効性の解析