人間と同じように考える機械を作るのは、人間の大きな夢であり、それができるかもしれないと言われているのが強化学習の枠組みです。強化学習は、ディープラーニングを取り入れることでめざましく進化してきました。今回は、そのディープラーニングを使って行う強化学習である深層強化学習を実践していきます。前回は、方策が離散的な場合の Actor Critic モデルを構築しました。そちらが気になる方は前回の記事を是非ご覧ください。
今回は、方策が連続値である場合の深層強化学習のモデルを実装します。方策が連続値と離散値ではモデルの作り方が異なります。離散値の場合は、Actor モデルにおいて選択手の確率を予測するように設計しましたが、連続値においてはそのやり方ではできません。連続値に対応するには一工夫が必要です。
今回の内容を実践してもらうと、振り子を立たせる行動を選択し続けるゲームにおいて、下記のようにうまく立たせられる行動選択をするモデルができます。実践用のコードはこちらに置いてあります。

連続値制御の Actor Critic モデルの概要
例えばゴルフの場合、カップまでの距離、風、体調など様々な変数を読み取り、体にどれくらいの力を入れるかを決めてドライバーを振り、ボールをカップに入れるように飛ばさなければいけません。環境の状態に応じて行動を決めなければいけませんが、この例でいえば行動とは体のどこにどれくらいの力を入れるかであり、連続値を扱うことになります。これが囲碁や将棋の強化学習モデルとは違うところです。

このように連続値制御に対応した強化学習のモデルが必要になります。そこで、Actor Critic の Actor 側を連続値が扱えるようにします。Actor では、状態を入力として受け取り、行動の平均と対数偏差を出力するようにします。この部分が離散値行動の場合との違いです。Critic では、状態と行動を入力として受け取り、Q値を出力するという定番の形です。

Actor を上記のように平均と対数偏差を出力させることで、それを使って正規分布によるランダムな行動選択ができるようになります。モデルの学習時において、Actor の出力値をそのまま行動としてしまうと行動の探索範囲が狭まってしまいます。これを防ぐために、Actor の出力値に対してランダム値を付加しています。

以上でモデルの概要に関する説明は終了です。次からモデルの実装をしていきます。
準備
モデルの実装に入る前に、必要なモジュールのインポートやディレクトリの準備をします。
必要なモジュールのインポート
今回使用するモジュールとして重要なのは、「gym」と「torch」です。「gym」は強化学習の環境を作るモジュールであり、「torch」はディープラーニングを構築するモジュールです。使用した主要なモジュールのバージョンは以下のとおりです。
| モジュール名 | バージョン |
|---|---|
| gym | 0.24.1 |
| torch | 1.11.0 |
| seaborn | 0.11.2 |
| numpy | 1.21.5 |
| pandas | 1.4.1 |
使用するモジュールをインポートします。
from pathlib import Path import random import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from tqdm import tqdm import gym import torch import torch.nn as nn import torch.nn.functional as F import torch.optim as optim from torch.distributions import Normal
パラメータの設定
今回実装する強化学習のゲームは、「gym」の「Pendulum」です。「Pendulum」は振り子を立たせ続けることを目的とし、振り子を立たせ続けるために -2 〜 2 の範囲で行動を選択します。「Pendulum」に関する詳しいことはこちらが参考になります。ここでは、今回行うゲーム名の設定や必要なディレクトリの作成を行っています。
gym_game_name = 'Pendulum-v1' device = torch.device("cuda" if torch.cuda.is_available() else "cpu") result_dir_path = Path('result') model_dir_path = Path('model') if not result_dir_path.exists(): result_dir_path.mkdir(parents=True) if not model_dir_path.exists(): model_dir_path.mkdir(parents=True)
モデルの設計
連続値制御をする Actor Critic モデルを構築していきます。Actor が特殊なのでここの理解が重要になります。
Critic の設計
Critic モデルは、状態とアクションを入力に受け取り、Q値を出力します。ネットワークの構造は通常のニューラルネットワークなので、難しくないです。
class CriticNet(nn.Module): def __init__(self, input_dim, output_dim, hidden_dim): super().__init__() self.linear1 = nn.Linear(input_dim, hidden_dim) self.linear2 = nn.Linear(hidden_dim, hidden_dim) self.linear3 = nn.Linear(hidden_dim, output_dim) def forward(self, state, action): x = torch.cat([state, action], 1) x = F.relu(self.linear1(x)) x = F.relu(self.linear2(x)) x = self.linear3(x) return x
Actor の設計
Actor は、状態を入力として受け取り、アクションの平均と対数偏差を出力します。アクションの出力の仕方が連続値制御の肝になっています。学習時において選択アクションにランダム性を持たせるため、出力した平均と対数偏差を使った正規分布をかましています。Actor が出力する値が基準となっていますが、学習時には正規分布に従ってランダム要素を付加しています。その際に必要になる偏差も Actor から出力させ、こちらも学習できるようにしています。
LOG_SIG_MAX = 2 LOG_SIG_MIN = -20 epsilon = 1e-6 class ActorNet(nn.Module): def __init__(self, input_dim, output_dim, hidden_dim, action_scale): super().__init__() self.linear1 = nn.Linear(input_dim, hidden_dim) self.linear2 = nn.Linear(hidden_dim, hidden_dim) self.mean_linear = nn.Linear(hidden_dim, output_dim) self.log_std_linear = nn.Linear(hidden_dim, output_dim) self.action_scale = torch.tensor(action_scale) self.action_bias = torch.tensor(0.) def forward(self, state): x = F.relu(self.linear1(state)) x = F.relu(self.linear2(x)) mean = self.mean_linear(x) log_std = self.log_std_linear(x) log_std = torch.clamp(log_std, min=LOG_SIG_MIN, max=LOG_SIG_MAX) return mean, log_std def sample(self, state): mean, log_std = self.forward(state) std = log_std.exp() normal = Normal(mean, std) x_t = normal.rsample() y_t = torch.tanh(x_t) action = y_t * self.action_scale + self.action_bias mean = torch.tanh(mean) * self.action_scale + self.action_bias return action, mean def to(self, device): self.action_scale = self.action_scale.to(device) self.action_bias = self.action_bias.to(device) return super().to(device)
Actor Critic の設計
Actor と Critic のそれぞれの設計ができたので、これらを組み合わせて連続値制御ができる Actor Critic モデルを構成していきます。この class でのポイントは以下のとおりです。
- Critic のコピー(学習しないネットワーク)を作成し、定期的に学習中の Critic のパラメータをコピー
- コピー Critic を使って、\(t + 1\) ステップの行動価値を予測し、それをもとに \( t \) ステップの行動価値を求める
- Critic は予測Q値と学習データから求まるQ値の差分が損失値であり、Actor は予測選択手から求まるマイナスQ値が損失値
class ActorCriticModel(object): def __init__(self, state_dim, action_dim, action_scale, args, device): self.gamma = args['gamma'] self.tau = args['tau'] self.alpha = args['alpha'] self.target_update_interval = args['target_update_interval'] self.device = device self.actor_net = ActorNet(input_dim=state_dim, output_dim=action_dim, hidden_dim=args['hiden_dim'], action_scale=action_scale).to(self.device) self.critic_net = CriticNet(input_dim=state_dim + action_dim, output_dim=1, hidden_dim=args['hiden_dim']).to(self.device) self.critic_net_target = CriticNet(input_dim=state_dim + action_dim, output_dim=1, hidden_dim=args['hiden_dim']).to(self.device) hard_update(self.critic_net_target, self.critic_net) convert_network_grad_to_false(self.critic_net_target) self.actor_optim = optim.Adam(self.actor_net.parameters()) self.critic_optim = optim.Adam(self.critic_net.parameters()) def select_action(self, state, evaluate=False): state = torch.FloatTensor(state).unsqueeze(0).to(self.device) if not evaluate: action, _ = self.actor_net.sample(state) else: _, action = self.actor_net.sample(state) return action.detach().numpy().reshape(-1) def update_parameters(self, memory, batch_size, updates): state_batch, action_batch, reward_batch, next_state_batch, mask_batch = memory.sample(batch_size=batch_size) state_batch = torch.FloatTensor(state_batch).to(self.device) next_state_batch = torch.FloatTensor(next_state_batch).to(self.device) action_batch = torch.FloatTensor(action_batch).to(self.device) reward_batch = torch.FloatTensor(reward_batch).unsqueeze(1).to(self.device) mask_batch = torch.FloatTensor(mask_batch).unsqueeze(1).to(self.device) with torch.no_grad(): next_state_action, _ = self.actor_net.sample(next_state_batch) next_q_values_target = self.critic_net_target(next_state_batch, next_state_action) next_q_values = reward_batch + mask_batch * self.gamma * next_q_values_target q_values = self.critic_net(state_batch, action_batch) critic_loss = F.mse_loss(q_values, next_q_values) self.critic_optim.zero_grad() critic_loss.backward() self.critic_optim.step() action, _ = self.actor_net.sample(state_batch) q_values = self.critic_net(state_batch, action) actor_loss = - q_values.mean() self.actor_optim.zero_grad() actor_loss.backward() self.actor_optim.step() if updates % self.target_update_interval == 0: soft_update(self.critic_net_target, self.critic_net, self.tau) return critic_loss.item(), actor_loss.item()
設計に必要な関数
ネットワークのパラメータをコピーする関数や学習しないように設定する関数を準備します。
def soft_update(target_net, source_net, tau): for target_param, param in zip(target_net.parameters(), source_net.parameters()): target_param.data.copy_(target_param.data * (1.0 - tau) + param.data * tau) def hard_update(target_net, source_net): for target_param, param in zip(target_net.parameters(), source_net.parameters()): target_param.data.copy_(param.data) def convert_network_grad_to_false(network): for param in network.parameters(): param.requires_grad = False
ここまででモデルの設計に必要なコードは完成です。次は、学習データを蓄えておくためのメモリの設計を行います。
メモリの設計
深層強化学習の良いところは、自分でプレイして得たデータを使って更に学習できることです。これを実現するためには、学習によって得られたデータを蓄えておくメモリが必要になります。メモリには、保存データに優先度をつける優先度メモリのような拡張方法もありますが、今回はシンプルに一定数だけの学習データを保存し、一定数を超えた場合は古いデータから消える設計にしています。
class ReplayMemory: def __init__(self, memory_size): self.memory_size = memory_size self.buffer = [] self.position = 0 def push(self, state, action, reward, next_state, mask): if len(self.buffer) < self.memory_size: self.buffer.append(None) self.buffer[self.position] = (state, action, reward, next_state, mask) self.position = (self.position + 1) % self.memory_size def sample(self, batch_size): batch = random.sample(self.buffer, batch_size) states, actions, rewards, next_states, dones = map(np.stack, zip(*batch)) return states, actions, rewards, next_states, dones def __len__(self): return len(self.buffer)
設計は以上になります。これらのコードを使い実際にモデルを学習させます。
連続値制御のActor Critic モデルの学習
上記まででモデルの設計するためのコードは完成です。後は、実際に Actor Ciritic モデルを学習させていきます。コードでは GPU にも対応していますが、ローカルでも実用的な時間で充分な学習が完了します。私の場合は、6分ほどで処理が終了しました。
学習コードは以下になりますが、特に複雑な処理はないかと思います。ある状態に対して行動を選択し、次の状態に対して行動を選択し、ということを繰り返しながらデータを貯めていき、メモリから「batch_size」分の学習データに対して学習を繰り返しています。
args = {
'gamma': 0.99,
'tau': 0.005,
'alpha': 0.2,
'seed': 123456,
'batch_size': 256,
'hiden_dim': 256,
'start_steps': 1000,
'target_update_interval': 1,
'memory_size': 100000,
'epochs': 100,
'eval_interval': 10
}
env = gym.make(gym_game_name)
agent = ActorCriticModel(
state_dim=env.observation_space.shape[0], action_dim=env.action_space.shape[0], action_scale=env.action_space.high[0],
args=args, device=device
)
memory = ReplayMemory(args['memory_size'])
episode_reward_list = []
eval_reward_list = []
n_steps = 0
n_update = 0
for i_episode in range(1, args['epochs'] + 1):
episode_reward = 0
done = False
state = env.reset()
while not done:
if args['start_steps'] > n_steps:
action = env.action_space.sample()
else:
action = agent.select_action(state)
if len(memory) > args['batch_size']:
agent.update_parameters(memory, args['batch_size'], n_update)
n_update += 1
next_state, reward, done, _ = env.step(action)
n_steps += 1
episode_reward += reward
memory.push(state=state, action=action, reward=reward, next_state=next_state, mask=float(not done))
state = next_state
episode_reward_list.append(episode_reward)
if i_episode % args['eval_interval'] == 0:
avg_reward = 0.
for _ in range(args['eval_interval']):
state = env.reset()
episode_reward = 0
done = False
while not done:
with torch.no_grad():
action = agent.select_action(state, evaluate=True)
next_state, reward, done, _ = env.step(action)
episode_reward += reward
state = next_state
avg_reward += episode_reward
avg_reward /= args['eval_interval']
eval_reward_list.append(avg_reward)
print("Episode: {}, Eval Avg. Reward: {:.0f}".format(i_episode, avg_reward))
print('Game Done !! Max Reward: {:.2f}'.format(np.max(eval_reward_list)))
torch.save(agent.actor_net.to('cpu').state_dict(), model_dir_path.joinpath(f'{gym_game_name}_actor.pth'))
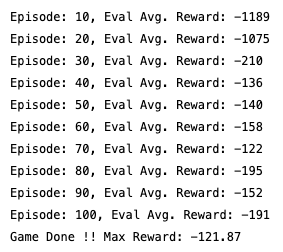
学習時に一定期間ごとに評価報酬の平均値を求めていました。こちらを可視化し、学習時が進むに連れ評価報酬が上がっているのかを確認します。
plt.figure(figsize=(8, 6), facecolor='white') g = sns.lineplot( data=pd.DataFrame({ 'episode': range(args['eval_interval'], args['eval_interval'] * (len(eval_reward_list) + 1), args['eval_interval']), 'reward': eval_reward_list }), x='episode', y='reward', lw=2 ) plt.title('{}エピソードごとの学習済みモデルにおける\n評価報酬の平均値の推移'.format(args['eval_interval']), fontsize=18, weight='bold') plt.xlabel('エピソード') plt.ylabel('獲得報酬の平均値') for tick in plt.yticks()[0]: plt.axhline(tick, color='grey', alpha=0.1) plt.tight_layout() plt.savefig(result_dir_path.joinpath('{}_eval_reward_{}.png'.format(gym_game_name, args['eval_interval'])), dpi=500)

学習済みモデルの検証
学習済みモデルの選択手がゲームの報酬を上げるように選ばれているのかを確認します。そのために、「学習済みモデルの行動選択」と「ランダムな行動選択」のそれぞれで100回ゲームをプレイし、獲得報酬の分布を比較してみます。
result = [] for experiment_name in ['agent', 'random']: for i in tqdm(range(100)): state = env.reset() episode_reward = 0 done = False while not done: if experiment_name == 'agent': with torch.no_grad(): action = agent.select_action(state, evaluate=True) else: action = env.action_space.sample() next_state, reward, done, _ = env.step(action) episode_reward += reward state = next_state result.append([experiment_name, i, episode_reward]) result = pd.DataFrame(result, columns=['experiment_name', 'i', 'reward']) g = sns.catplot(data=result, x='experiment_name', y='reward', kind='boxen') g.fig.suptitle('学習済みモデルとランダムの報酬の比較', fontsize=18, weight='bold', y=1.0) g.fig.set_figwidth(8) g.fig.set_figheight(6) g.fig.set_facecolor('white') g.set_xlabels('') g.set_ylabels('') g.set_xticklabels(fontsize=16) g.tight_layout() g.savefig(result_dir_path.joinpath(f'{gym_game_name}_reward_agent_vs_random.png'), dpi=500)

上手を見てもらえば分かる通り、学習済みモデルの方がランダムよりも遥かに高い報酬になっています。連続値を制御する Actor Critic モデルができていることがわかります。
終わりに
今回は実装の話が中心でしたが、強化学習の理論面を詳しく学びたいという方は下記の本が非常に参考になりましたので、ご覧ください。
