前回は統計的検定ってなんなの？っていうのをイメージで語ってみました。検定を作業と考えてなんとなくやりきってきた方々はぜひご一読ください。
www.dskomei.com
検定をイメージで語ってみたわけですが、やはり実際にやってみないと腹落ちしないですよね。ということで、今回はt検定をしてみたいと思います。ただいきなりt検定をしても作業で終わってしまうので、背景を抑えながら理解していきたいと思います。
検定をやる上で大事なことは観測値が確率分布に従うことでした。何故かと言うと、観測値が過去の値とは比べ物にならないくらい良いと言ったときに、どのくらいの差をすごいと言っているのかが人によって異ってしまうと困りますよね。MTG中に2人の上司が意味ある・ないを言い争っていたら、新卒はとりあえずネットサーフィンでもしますよね。なので、意味がある差か否かを数値的に表現する必要があります。観測値が従う確率分布において、その値が観測される確率は◯％です。だからすごい稀なことが起きているよ！という形で。ここで大事になってくるのが、現実世界の色んな場面で観測される値が従う確率分布なんてあるのかということです。まさしくそれが、正規分布です。
正規分布
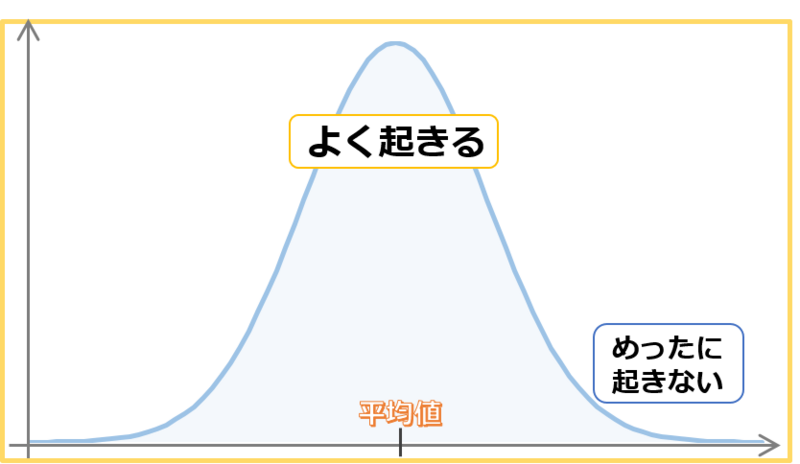正規分布は平均を中心とした左右対称な釣鐘状の分布とよく言われますが、イメージを持つために実際の形を見てみましょう。横軸の中心が平均であり、そこが山になっています。これは確率分布なので、この山になっている平均値がこの母集団において最もよく観測され得るということを意味しています。そして平均から離れるにつれ、縦軸の値が低くなっていきます。これは、平均値から離れた値のものは観測されにくいということです。つまり正規分布は、平均値付近の値はよく観測され、平均値から離れている値は観測されづらいということを表す分布なのです。
正規分布では観測値の確率がわかりますが、それは数式で描けるからにほかなりません。数式で描けない場合はというと、機械学習の出番になりますがその話は一旦置いといて。正規分布に置いて確率変数を\(X\)、母平均を\(μ\)、母標準偏差を\(σ\)とすると、以下の式になります。\(x\)は確率変数\(X\)の取り得る値です。
正規分布をpythonで描く
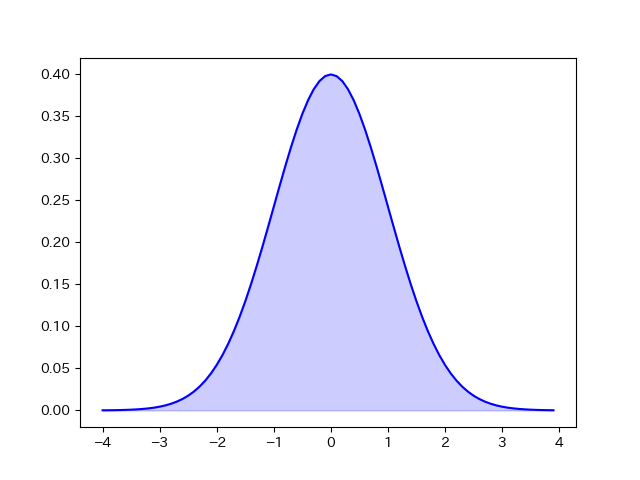正規分布の確率を得るために『scipy』ライブラリを使っています。右のグラフは母平均０、母標準偏差1の正規分布を描いています。このグラフを描くコードは以下のとおりです。
from pathlib import Path from scipy.stats import norm import numpy as np import matplotlib.pyplot as plt image_dir_path = Path('./image') if not image_dir_path.exists(): image_dir_path.mkdir(parents=True) x = np.arange(-4, 4, 0.1) # 平均0、標準偏差１の正規分布から入力データの確率を得ている y = norm.pdf(x=x, loc=0, scale=1) plt.plot(x, y, 'b') plt.fill_between(x, y, color='b', alpha=0.2) plt.savefig(image_dir_path.joinpath('norm.png').__str__()) plt.show()
正規分布を使って検定
平均50点、標準偏差10だったテストにおいて各点数がどのような確率になるかを見てみましょう。勘の鋭い方ならおわかりかと思いますが、学生の頃に苦しめられた偏差値のことです。偏差値とは各テストに置いて平均を50点、標準偏差を10として、得点を標準化した値のことです。
cdf関数は指定した平均値、標準偏差の正規分布における累積確率密度関数になります。分布の左からの確率が得られるので、下の例では、ある得点だと上位◯%とするために、1からcdf関数の値を引いています。
from scipy.stats import norm # 平均50、標準偏差60の正規分布 x = 60 y = norm.cdf(x=x, loc=50, scale=10) print('得点{}は上位{:.2f}%'.format(x, (1-y)*100)) x = 80 y = norm.cdf(x=x, loc=50, scale=10) print('得点{}は上位{:.2f}%'.format(x, (1-y)*100)) x = 40 y = norm.cdf(x=x, loc=50, scale=10) print('得点{}は上位{:.2f}%'.format(x, (1-y)*100))
実装結果は以下のようになります。上位5%をすごい人とすると、得点80は異常にすごい人ということになります。
得点60は上位15.87% 得点80は上位0.13% 得点40は上位84.13%
標準化
正規分布は得られた値の確率がわかるため非常に便利なのですが、平均や分散の値によって分布が変わるため、同じ縦軸・横軸を使った分布の比較ができません。これを可能にするためにデータを変換してしまうのが標準化です。平均0、標準偏差1になるようにデータを変換します。標準化したあとの値（標準化変量）を\(z\)とすると、標準化をするための式は以下になります。ここで、\(z\)値に従う分布で行う検定をz検定と呼びます。
なんで観測値から平均を引いて標準偏差で割れば標準化されるのか気になった方は以下の本をご覧ください。数式の展開の流れが平易な言葉で書かれているので、数式が苦手な方でもたやすく理解できると思います。
t値の導出
t検定は巷でよく聞きます。それはt検定が実用的な検定だからです。先程のz検定だと、母集団の分散がわかっていないといけません。しかし、母集団の分散なんてなかなかわかりません。周りにいる人の身長から平均身長を求めることは簡単ですが、日本中にいる人の全員の身長を聞いて回るのは大変です。そこで標本集団から分散を求めるわけですが、標本から求める分散は母分散からすると大きくなってしまうことがあります。標本に偏りが出てきてしまうからです。よって、標本から求めた分散は、通常の分散を求める式とは異なり分母をn-1とします。この分散のことを不偏分散\(\sigma^2\)と呼び、式は以下のとおりです。
大事なこととして、検定は、観測値が何かしら数式であらわせる確率分布に従っていないと行えません。なので、適当な標本を持ってきても検定を行うことはできません。ただ、平均値の分布はサンプルサイズが大きくなるに連れ正規分布に従います。これを中心極限定理と呼びます(*1)。標本の平均値に関する検定ならば、確率がわかるため行えるということです。
標本の標準偏差を\(s\)とすると、標本分散は\(s^2\)ですが、標本平均の分散は\(\frac{s^2}{n}\)になります。これは計算で確かめられますのでぜひお試しください。こちらに詳しく書かれています。これらのことを合わせると、t値は以下のようになります。
t検定
t値の導出が終わりましたので、具体例をもとに検定をしていきたいと思います。
ある店で先週から模様替えをしたところ、各曜日において月曜日から以下の順で人数が増減しました。これは効果があったと言えるのでしょうか？
人数の増減値：[10, -10, 40, -5, 5-, 50, 40]
この疑問をt検定で判明させたいと思います。以下が実装コードです。
from scipy.stats import t import numpy as np # 例題の数字列 x = [10, -10, 40, -5, 50, 50, 40] x = np.array(x) x_mean = x.mean() # numpyのデフォルトでは標準偏差なため, # 引数ddof=1を指定して不偏標準偏差とする x_std = x.std(ddof=1) # t値の導出 t_value = (x_mean-0) / (x_std / np.sqrt(x.size)) # 自由度n-1のt分布から確率を求めている y = t.pdf(x=t_value, df=x.size-1) # alphaで指定した範囲のt値の上下限を求めている alpha = 0.95 intervals = t.interval(alpha=alpha, df=x.size-1) print('標本平均={:.2f}, 不偏標準偏差={:.2f}'.format(x_mean, x_std)) print('t分布における確率={:.2f}%'.format((1-y)*100)) print('標本のt値={:.2f} {}%のt値の範囲:({:.2f},{:.2f})'.format(t_value, int(alpha*100), intervals[0],intervals[1]))
実装した結果は以下のようになりました。両側5%で検定した結果、t値は2.55となり自由度6のt分布の95%範囲のt値を超えています。今回の人数の増え幅は有意な差があることがわかりました。店内の模様替えを更にド派手にしたほうが良さそうですね。
標本平均=25.00, 不偏標準偏差=25.98 t分布における確率=97.05% 標本のt値=2.55 95%のt値の範囲:(-2.45,2.45)
終わりに
検定は自分の中ではややこしくて苦手でしたが、一から勉強してみると、数字の羅列に新たな情報を付与するものであり、大いに役に立つと感じました。すごい差がある！めっちゃ良い！などの言葉が聞こえてきたら検定をしたくなりますよね。検定を概念から勉強する上で、以下の本にお世話になりました。感謝いたします。
