今回は、答えのないデータから、データの構造を見えるようにするクラスタリングについて述べていきます。クラスタリングとは、データが似ているものを一つのクラスタにまとめて情報を集約することによって、見通しを良くするものです。例えば、人の特徴を一人一人見るよりは、性別や世代にまとめて比較した方がわかりやすいです。
クラスタリングでよく使われるのはk-meansであり、k-meansに関する詳しいことは様々なところで述べられています。なので、このエントリではk-meansではなく、k-medoidsという手法に焦点を当てます。k-medoidsを一言で言えば外れ値に強いです。詳しいことは後ほど見ていきます。
今回は、k-medoidsに関して、分類後のクラスタの評価・初期化の改良・クラスタ数の自動決定を行っていきます。本エントリでは階層クラスタリングについての説明はないため、クラスタリングと言った場合に非階層クラスタリングを指しています。今回のエントリーを読むと下図のようなことができます。


- k-medoidsを学ぶ前にk-meansをおさらい 王道
- k-meansの問題 シンプルであるからこそ
- k-medoidsとは
- クラスタリングの評価 直感と数字の間に悩む
- クラスタリングにおける初期化 はじめの一歩でケリをつける
- クラスタ数決定の自動化 寝てる間にクラスタリング
- 参考文献
k-medoidsを学ぶ前にk-meansをおさらい 王道
クラスタリング手法の王様と言っても良いくらい有名なk-meansに関して、軽くおさらいをします。k-meansでは、分割したいクラスタ数を与えたら、各ノードがどこかのクラスタに分類されることを目指します。学生の頃の学年の切り替わりと共に行われるクラス分けを思い出してもらえれば良いと思います。分割したいクラス数が事前に決まっていて、何かしらの基準によって分けられていました。あの頃は、気になる人と同じクラスになれるかドキドキしましたね。今思うと、同じクラスになれたということはクラスタリング的には距離が近かったということですね。それはさておき、分割したいクラスタ数を\(k\)として、k-meansの処理を以下に記述します。
- 各点をランダムに\(k\)個のクラスタのどれかに割り当てる
- 各クラスタの重心を求める
- 各点を一番近い重心のクラスタに再度割り当て直す
- 3.においてクラスタの再割当てをするノードがなければ終了し、あれば2.に戻る

pythonではk-measnは、sklearnライブラリに既に組み込まれてり、簡単にk-meansを実行することができます。先に結果のグラフを表示します。データ自体が分けやすいようになっていることもあり、分類したいクラスタ数に的確にクラスタリングされていることがわかります。

k-meansの実装は以下のようになります。
from pathlib import Path import numpy as np from sklearn.datasets import make_blobs import matplotlib.pyplot as plt from sklearn.cluster import KMeans image_dir_path = Path('./image') if not image_dir_path.exists(): image_dir_path.mkdir(parents=True) # 分類したいクラスタ数をいろいろ変えて試してみる n_clusters = [2, 3, 4, 5] colors = ['lightgreen', 'orange', 'lightblue', 'hotpink', 'yellow'] markers = ['s', 'o', 'v', 'h', 'p'] for plot_num, n_cluster in enumerate(n_clusters): # 指定したクラスタ数のデータを作ってくれる # cluster_stdでデータの散らばり具合を調整できる x_data, labels = make_blobs(n_samples=150, n_features=2, centers=n_cluster, cluster_std=1.5, shuffle=True, random_state=0) # k-meansは一行で行える # n_clustersでクラスタ数を指定し、initで初期化方法を指定している # initの初期化は「k-means++」であり、これは後ほど説明する km = KMeans(n_clusters=n_cluster, init='random') predicted_labels = km.fit_predict(x_data) centroids = km.cluster_centers_ # クラスタリング結果の可視化 plt.subplot(2, 2, plot_num+1) for i, label in enumerate(sorted(np.unique(predicted_labels))): # 分類した結果のクラスをプロット plt.scatter(x_data[predicted_labels==label, 0], x_data[predicted_labels==label, 1], c=colors[i], marker=markers[i], s=15) # 最終的なセントロイドをプロット plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='*', s=70) plt.title('n cluster '+str(n_cluster)) plt.tight_layout() plt.savefig(image_dir_path.joinpath('k_means.png').__str__()) plt.show()
ただ、k-meansには問題があります。全知全能な手法というものはなかなかないものです。では、その問題を次に見ていきたいと思います。
k-meansの問題 シンプルであるからこそ
k-meansの問題としては、以下のことがよく言われています。
- k-meansは座標をクラスタの重心(セントロイド)とするため、外れ値の影響を受けやすい
- k-meansの結果できたクラスタは、どのようになれば良いクラスタかを判断するかが明確ではない
- クラスタリングの結果は初期化時のランダム処理に依存する
- 最初にクラスタ数を指定しなければいけないが、クラスタ数は決まっていないことが多い
言うなれば、よく分類してくれればクラスタ数は何でも良い
1.を解決するのがまさしく『k-medoids』です。そこで、k-medoisとはうんたらという話に入っていくわけですが、2.~4.に関しては、k-meansの問題というよりはクラスタリングで起こる問題であり、k-medoidsでも考慮しなければいけないことです。そこで、これらに関しては、k-meansで問題を解決するために行われた改良をk-medoidsに取り込んでいくという形で両方見ていきます。炭水化物 on 炭水化物という広島焼き戦法です。
k-medoidsとは
k-meansはよく聞いたことがあるけど、k-medoidsは全く聞いたことがないからといって力むことはありません。言っていることの本質はk-meansと変わりませんし、方法も似通っています。それでは処理を見てみます。先ほどと同じように、分割したいクラスタ数を\(k\)とします。
- \(k\)個のクラスタ数分の点をランダムに選択する(medoid)
- 各点を一番近いmedooidのクラスタに割り当てる
- それぞれのクラスタ内において、クラスタ内の他のすべての点との距離の合計が最小になる点を新たにmedoidとする
- 3.においてmedoidに変化がなければ終了し、あれば2.に戻る
クラスタ\(i\)の要素の集合を\(X_i \)とし、距離関数を\(d()\)とすると、新しいmedoidを求める式は次式になります。

ただ、k-medoidsはsklearnの中にはまだないようです。そこで、k-medoidsを自作してみたいと思います。k-meansと同じように実行できるように、class化します。
from pathlib import Path import numpy as np import pandas as pd from sklearn.datasets import make_blobs from scipy.spatial.distance import pdist, squareform import matplotlib.pyplot as plt image_dir_path = Path('./image') if not image_dir_path.exists(): image_dir_path.mkdir(parents=True) class KMedoids(object): def __init__(self, n_cluster, max_iter=300): self.n_cluster = n_cluster self.max_iter = max_iter def fit_predict(self, D): m, n = D.shape initial_medoids = np.random.choice(range(m), self.n_cluster, replace=False) tmp_D = D[:, initial_medoids] # 初期セントロイドの中で距離が最も近いセントロイドにクラスタリング labels = np.argmin(tmp_D, axis=1) # 各点に一意のIDが振ってあった方が分類したときに取り扱いやすいため # IDをもつようにするデータフレームを作っておく results = pd.DataFrame([range(m), labels]).T results.columns = ['id', 'label'] col_names = ['x_' + str(i + 1) for i in range(m)] # 各点のIDと距離行列を結びつかせる # 距離行列の列に名前をつけて後々処理しやすいようにしている results = pd.concat([results, pd.DataFrame(D, columns=col_names)], axis=1) before_medoids = initial_medoids new_medoids = [] loop = 0 # medoidの群に変化があり、ループ回数がmax_iter未満なら続く while len(set(before_medoids).intersection(set(new_medoids))) != self.n_cluster and loop < self.max_iter: if loop > 0: before_medoids = new_medoids.copy() new_medoids = [] # 各クラスタにおいて、クラスタ内の他の点との距離の合計が最小の点を新しいクラスタとしている for i in range(self.n_cluster): tmp = results.ix[results['label'] == i, :].copy() # 各点において他の点との距離の合計を求めている tmp['distance'] = np.sum(tmp.ix[:, ['x_' + str(id + 1) for id in tmp['id']]].values, axis=1) tmp = tmp.reset_index(drop=True) # 上記で求めた距離が最初の点を新たなmedoidとしている new_medoids.append(tmp.loc[tmp['distance'].idxmin(), 'id']) new_medoids = sorted(new_medoids) tmp_D = D[:, new_medoids] # 新しいmedoidのなかで距離が最も最小なクラスタを新たに選択 clustaling_labels = np.argmin(tmp_D, axis=1) results['label'] = clustaling_labels loop += 1 # resultsに必要情報を追加 results = results.ix[:, ['id', 'label']] results['flag_medoid'] = 0 for medoid in new_medoids: results.ix[results['id'] == medoid, 'flag_medoid'] = 1 # 各medoidまでの距離 tmp_D = pd.DataFrame(tmp_D, columns=['medoid_distance'+str(i) for i in range(self.n_cluster)]) results = pd.concat([results, tmp_D], axis=1) self.results = results self.cluster_centers_ = new_medoids return results['label'].values # 分類したいクラスタ数をいろいろ変えて試してみる n_clusters = [2, 3, 4, 5] colors = ['lightgreen', 'orange', 'lightblue', 'hotpink', 'yellow'] markers = ['s', 'o', 'v', 'h', 'p'] for plot_num, n_cluster in enumerate(n_clusters): # 指定したクラスタ数のデータを作ってくれる # cluster_stdでデータの散らばり具合を調整できる x_data, labels = make_blobs(n_samples=150, n_features=2, centers=n_cluster, cluster_std=1.5, shuffle=True, random_state=0) # k-meansと同じように初期化ではクラスタ数を指定する km = KMedoids(n_cluster=n_cluster) # k-medoidsの利点として、座標がなくても距離行列があればクラスタリングができるので # (k-meansの場合は座標が必要)行列を入力データとしている # そのため、データを行列に変えている D = squareform(pdist(x_data, metric='euclidean')) predicted_labels = km.fit_predict(D) centroids = km.cluster_centers_ # クラスタリング結果の可視化 plt.subplot(2, 2, plot_num+1) for i, label in enumerate(sorted(np.unique(predicted_labels))): # 分類した結果のクラスをプロット plt.scatter(x_data[predicted_labels==label, 0], x_data[predicted_labels==label, 1], c=colors[i], marker=markers[i], s=15) # medoidはノード番号なため、元データからプロット座標を得ている plt.scatter(x_data[centroids, 0], x_data[centroids, 1], c='red', marker='*', s=70) plt.title('n cluster '+str(n_cluster)) plt.tight_layout() plt.savefig(image_dir_path.joinpath('k_medoids.png').__str__()) plt.show()
実行結果は以下のグラフのようになりました。k-meansによるクラスタリングと結果は違わないように見えます。
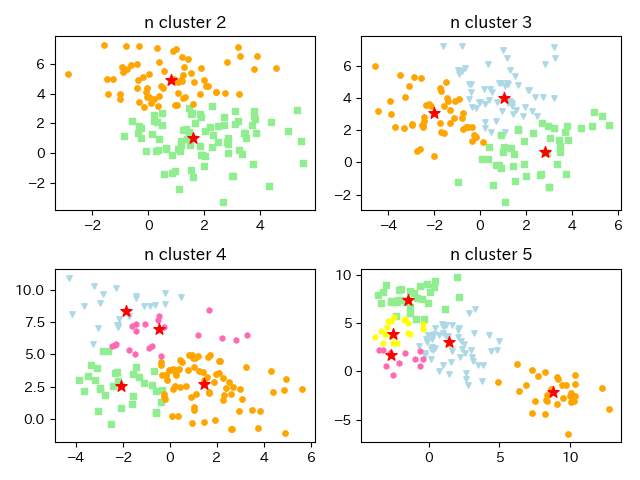
k-meansとk-medoidsは何が違うかをおさらいすると、クラスタリングの基点となる点を座標とするのがk-meansで、点そのものとするのがk-medoidsです。k-meansは座標を見るため外れ値の座標の影響を受けますが、k-medoidsは点そのもので見るため遠い距離にある外れ値の影響を受けません。これは、平均値と中央値の関係によく似ています。
また、k-medoidsには利点がもうひとつあります。それは、座標がわからなくても各点の距離が分かればクラスタリングできることです。このことは集合での距離にもとづいてクラスタリングをしたいときに便利です。集合での距離作る例としてJaccard係数(*2)があります。距離行列だけわかればいいので、実際の座標がなくても距離行列ができるように自作すれば、クラスタリングできるようになります。
クラスタリングの評価 直感と数字の間に悩む
k-means、k-medoidsの両方でクラスタリングをできるようになったわけですが、どのクラスタリングがいいかをどのように決めれば良いでしょうか。デザイナ的視点の強い方は、人の顔に近いようなクラスタに魅了されるかもしれませんし、引っ込み思案の方は一つの要素で独立しているクラスタに何かしらのシンパシーを感じるかもしれません。そんな事を言っていると、一向に決まりそうにありませんので、やはりこれだという指標がほしいですよね。
クラスタリングということなので、クラスタ内の点がまとまっていたら良さそうですね。言い換えるならば、クラスタ内の基点の中心付近に集まっていたら良さそうですよね。つまり、各クラスタ内において、セントロイド(or medoid)からの距離の合計が小さければ良いクラスタリングということになります。これは、クラスタ内誤差平方和として表されます。ここで、クラスタを\(i\)として、\(k\)はクラスタ数、\(X_i\)はクラスタ\(i\)の要素の集合、\(\mu_i\)はクラスタ\(i\)のセントロイド(or medoid)を表しています。
クラスタを評価できるようになったことで、クラスタ数をいくつにすればよいかといことにも何かしらの情報を得られます。つまり、クラスタ数を変えて誤差平方和を比較すればよいのです。これをエルボー法と呼びます。一つの指標があるだけでも見えるようになることで思考が前進します。それでは、以下でエルボー法の例を見てみましょう。

今回はこれを実装するにあたって、k-medoidsの実装クラスをもつk_medoids.pyというファイル作り(最終的なコード)、最初にインポートしています。そのk-medoidsのクラス内に、クラスタ内誤差平方和(sse)を計算するclass関数を用意しています。
# # クラスタ内誤差平方和を求める関数 # def sse(self, distances, predicted_values, medoids): unique_labels = sorted(np.unique(predicted_values)) sse = [] for label, medoid in zip(unique_labels, medoids): # 各クラスタの中心からの距離 distance = distances[medoid, predicted_values == label] distance_squared = distance * distance sse.extend(distance_squared.tolist()) return np.sum(sse)
エルボー法でクラスタ内におけるまとまり具合を確認したわけですが、他のクラスタとの関連性を踏まえた指標も見ておきたいですね。クラスタ内ではまとまっているように見えても、ある点では他のクラスタの要素との距離の方が近かったということもあるかもしれません。まさしく、内通者がいるような状況かもしれませんね。そこで、クラスタ内の各点との距離(凝集度)と最も近いクラスタ内の各点との距離(乖離度)を比較してみることにします。凝集度が乖離度より小さければ、良いクラスタということになります。この比較方法がシルエット法です。以下がそのプロセスです。
- サンプル\(x_{i}\)とそのサンプルのクラスタ内との平均距離を求める
これを、凝集度と呼ぶ - サンプル\(x_{i}\)に最も近いクラスタ内のすべてのサンプルとの平均距離を求める
これを、乖離度と呼ぶ - クラスタの凝集度と乖離度との差を、それらのうちの大きい方で割り、シルエット係数を求める
\(s_{i}\)をシルエット係数とすると、次式になる。
シルエット係数の結果を見てみましょう。

赤い点線がシルエット係数の平均を表しています。グラフでのシルエット係数の分布に加えて、シルエット係数の平均を比較することでクラスタリングの良し悪しを判断できます。今回の結果からすると、一番良いクラスタリングといえるのはクラスタ数が2のときのようです。今回のコードは以下になります。
from pathlib import Path import numpy as np from sklearn.datasets import make_blobs from sklearn.cluster import KMeans from k_medoids import KMedoids from scipy.spatial.distance import pdist, squareform import matplotlib.pyplot as plt from matplotlib import cm import math image_dir_path = Path('./image') # # シルエット係数を求める関数 # def silhouette_samples(distances, labels): n_unique_label = sorted(np.unique(labels)) n_samples_per_label = np.bincount(labels, minlength=len(n_unique_label)) intra_clust_dists = np.zeros(distances.shape[0], dtype=distances.dtype) inter_clust_dists = np.inf + intra_clust_dists for curr_label in range(len(n_unique_label)): mask = labels == curr_label current_distances = distances[mask] # クラス内の対象点以外の点数のため-1をしている n_samples_curr_lab = n_samples_per_label[curr_label] - 1 if n_samples_curr_lab != 0: # クラス内の平均距離の集計 intra_clust_dists[mask] = np.sum(current_distances[:, mask], axis=1) / n_samples_curr_lab # 対象点と対象点が属さないクラスの最小平均距離を求めている for other_label in range(len(n_unique_label)): if other_label != curr_label: other_mask = labels == other_label other_distances = np.mean(current_distances[:, other_mask], axis=1) inter_clust_dists[mask] = np.minimum(inter_clust_dists[mask], other_distances) sil_samples = inter_clust_dists - intra_clust_dists sil_samples /= np.maximum(intra_clust_dists, inter_clust_dists) # クラスタ内の大きさが1のものは0に変換 sil_samples[n_samples_per_label.take(labels) == 1] = 0 return sil_samples n_clusters = np.arange(2, 11, 1) base_num = int(math.sqrt(len(n_clusters))) # シルエット係数をクラスタ数間で比較するため、x軸をシェアする fig, axs = plt.subplots(base_num, base_num, figsize=(8, 6), sharex=True) for plot_num, n_cluster in enumerate(n_clusters): x_data, labels = make_blobs(n_samples=150, n_features=2, centers=n_cluster, cluster_std=1., shuffle=True, random_state=0) km = KMedoids(n_cluster=n_cluster, max_iter=300) D = squareform(pdist(x_data, metric='euclidean')) predicted_labels = km.fit_predict(D) unique_labels = np.unique(predicted_labels) unique_labels.sort() # シルエット係数を求める silhouette_values = silhouette_samples(D, predicted_labels) ax = axs[math.floor(plot_num / base_num), int(plot_num % base_num)] y_ax_lower, y_ax_upper = 0, 0 yticks = [] for i, label in enumerate(unique_labels): silhouette_values_ = silhouette_values[predicted_labels == label] silhouette_values_.sort() color = cm.jet(i / n_cluster) y_ax_upper += len(silhouette_values_) ax.barh(range(y_ax_lower, y_ax_upper), silhouette_values_, height=1.0, edgecolor='none', color=color) yticks.append((y_ax_lower + y_ax_upper) / 2) y_ax_lower += len(silhouette_values_) silhouette_avg = np.mean(silhouette_values) print('clusters {} , silhouette avg : {:.2f}'.format(n_cluster, silhouette_avg)) # シルエット係数の平均値を点線でプロット ax.axvline(silhouette_avg, color='red', linestyle='--') ax.set_yticks(yticks) ax.set_yticklabels(unique_labels+1) ax.set_title('n cluster : '+str(n_cluster)) plt.tight_layout() plt.savefig(image_dir_path.joinpath('shilhouette.png').__str__()) plt.show()
シルエット係数は1に近いほどよいのですが、今回はクラスタ数が2のときが最高値であり、それでも0.55でした。もう少し改善したいところです。こういうときは、原点に戻って考え直すのが一番ですね。ということで、初期化について次に考えてみます。
クラスタリングにおける初期化 はじめの一歩でケリをつける
クラスタリングは基点となる点に基づいて行われるため、基点の位置で結果が変わります。なので、最初にどの点を基点として始めるかで結果の良し悪しは異なってきます。つまり、初期化が重要です。初期化されたところから修正していくため、最初に変なところにあったら、修正と言ってもたかが知れています。議題の設定が抽象的すぎで話をしても何も決まらないMTGと同じです。MTGは最初の議題でほぼ決まりですよね。クラスタリングにおける適切な初期化とは、基点同士にばらつきがあることです。その方法のひとつが「k-means++」です。以下がプロセスです。
- すべての点の中からセントロイドをランダムに一つ選択する
- 残りの点において、最近傍中心との距離\(D(x)\)を計算する
- 残りのデータ点から確率分布\( \frac{D(x)^2}{\sum D(x)^2}\)に従いランダムに一つ点を選択
- 指定したクラスタ数になるまで2.3.を繰り返す
ここで最近傍中心とは、ある点においてセントロイドの中で最も近いもののことを指します。ランダム選択の確率分布は最近傍中心との距離が大きくなるほど選択されやすくなっています。つまり、k-means++でやろうとしている初期化は、ランダム性を保ちながらセントロイド同士の距離感を近すぎないように保つことです。まさしく、西部劇での早打ちの決闘ですね。これまでのランダムにより選択された単純な初期化のセントロイドと上記の方法に基づいた初期化のセントロイドを比較してみましょう。

k-means++の初期化の方が単純なランダムな初期化よりもセントロイドにばらつきがあることが見られました。初期化が改善されていることがわかります。実際は、複数個の初期化からクラスタリングしたときにもっともクラスタ内誤差が小さかったクラスタリング結果を選ぶようです。上記の初期化方法を実装したものを下記に記載します。k-medoidsで使うために、入力データは距離行列に変換しています。
from pathlib import Path import numpy as np import pandas as pd from sklearn.datasets import make_blobs from scipy.spatial.distance import pdist, squareform import matplotlib.pyplot as plt image_dir_path = Path('./image') # # k-means++の初期化を行う関数 # def making_initial_medoids(distances, n_cluster): m, n = distances.shape distances_pd = pd.DataFrame({'id':range(m)}) distances_pd = pd.concat([distances_pd, pd.DataFrame(distances, columns=[i for i in range(n)])], axis=1) medoids = [] for cluster_num in range(n_cluster): if cluster_num == 0: medoid = np.random.randint(0, m, size=1) medoids.extend(medoid) else: distance = distances_pd.drop(medoids, axis=0) distance = distance.ix[:, ['id'] + medoids] # 最近傍中心を求めている distance['min_distance'] = distance.min(axis=1) distance['min_distance_squared'] = distance['min_distance']*distance['min_distance'] ids = distance['id'].values # 確率分布を求めている distance_values = distance['min_distance_squared'] / np.sum(distance['min_distance_squared']) medoid = ids[np.random.choice(range(ids.size), 1, p=distance_values)] medoids.extend(medoid) medoids = sorted(medoids) return medoids if __name__ == '__main__': n_cluster = 3 x_datas, labels = make_blobs(n_samples=150, n_features=2, centers=n_cluster, cluster_std=1., shuffle=True, random_state=0) unique_labels = np.unique(labels) D = squareform(pdist(x_datas, metric='euclidean')) colors = ['lightgreen', 'orange', 'lightblue'] markers = ['s', 'o', 'v'] for plot_num in range(9): initial_plus2 = making_initial_medoids(D, n_cluster=n_cluster) initial_normal = np.random.choice(range(x_datas.shape[0]), n_cluster, replace=False) plt.subplot(3, 3, plot_num+1) for i, label in enumerate(unique_labels): plt.scatter(x_datas[labels == label, 0], x_datas[labels == label, 1], c=colors[i], marker=markers[i], s=5, label='cluster %s'%label) plt.scatter(x_datas[initial_plus2, 0], x_datas[initial_plus2, 1], c='red', marker='*', s=100, label='initial++') plt.scatter(x_datas[initial_normal, 0], x_datas[initial_normal, 1], c='green', marker='*', s=100, label='initial normal') plt.legend(bbox_to_anchor=(1, 1), loc='best', borderaxespad=0) plt.tight_layout() plt.savefig(image_dir_path.joinpath('initial_plus2.png').__str__(), bbox_inches='tight') plt.show()
ただ、これはクラスタ数を固定して比較していますが、なぜこのクラスタ数なのかと言われると、答えに窮してしまいます。エルボー法やシルエット分析によって、グラフを見ながらクラスタ数を決めると言った試行錯誤をすれば確かにある程度の根拠を持って決められますが、やはり自動化したいですよね。では、クラスタ数決定の自動化に関して見てみましょう。
クラスタ数決定の自動化 寝てる間にクラスタリング
自動的にクラスタ数を決めると言っても、占い師が北に向かいなさいというようにデータを見たただけで最適なクラスタ数が点から降りてくるなんてことはありません。結局は、いくつかのクラスタ数を同一指標で比較して最も良い値だったクラスタ数を選択するということに他なりません。それを自動でやってくれるのであれば便利ですよね。今回はクラスタ数の自動決定アルゴリズムとして、x-meansを取り上げます。以下が処理方法です。こちらの論文を参考にしています。
- k-meansを使って2つのクラスタに分ける
- 分割したクラスタそれぞれにおいてk-meansで2つに分け、その際ににBICが良くなるならばそのままにし、悪くなるならば分割前のクラスタに戻して、このクラスタの分割を終了する
- 2.を再帰的に繰り返し、分割が終われば終了

今回はこれをk-medoids版に拡張したいと思います。とは言っても、距離行列に置き換えたときに上手く動作しなかったので、距離行列を入力データとしたx-medoidsは断念しました。なので、x-meansのk-meansの部分をk-medoidsに置き換えているだけです。早速実行結果を見てみましょう。

左のグラフが元のデータであり、そのデータをクラスタリングしており、右のグラフが同じクラスタ数に分類できておれば成功と言えます。上のグラフの通り、クラスタ数3~5において適切なクラスタ数に分類できていることがわかります。コードは以下のとおりです。
|from pathlib import Path import numpy as np from scipy import stats import pandas as pd import matplotlib.pyplot as plt from sklearn.cluster import KMeans from k_medoids import KMedoids from sklearn.datasets import make_blobs from scipy.spatial.distance import pdist, squareform image_dir_path = Path('./image') class XMedoids: def __init__(self, n_cluster=2, max_iter=9999, n_init=1): self.n_cluster = n_cluster self.max_iter = max_iter self.n_init = n_init def fit(self, X): self.__clusters = [] clusters = self.Cluster.build(X, KMedoids(n_cluster=self.n_cluster, max_iter=self.max_iter, n_init=self.n_init).fit(squareform(pdist(X)))) self.__recursively_split(clusters) self.labels_ = np.empty(X.shape[0], dtype=np.intp) for i, c in enumerate(self.__clusters): self.labels_[c.index] = i self.cluster_centers_ = np.array([c.center for c in self.__clusters]) self.cluster_log_likelihoods_ = np.array([c.log_likelihood() for c in self.__clusters]) self.cluster_sizes_ = np.array([c.size for c in self.__clusters]) return self def __recursively_split(self, clusters): for cluster in clusters: if cluster.size <= 3: self.__clusters.append(cluster) continue k_means = KMedoids(2, max_iter=self.max_iter, n_init=self.n_init).fit(squareform(pdist(cluster.data))) c1, c2 = self.Cluster.build(cluster.data, k_means, cluster.index) beta = np.linalg.norm(c1.center - c2.center) / np.sqrt(np.linalg.det(c1.cov) + np.linalg.det(c2.cov)) alpha = 0.5 / stats.norm.cdf(beta) bic = -2 * (cluster.size * np.log( alpha) + c1.log_likelihood() + c2.log_likelihood()) + 2 * cluster.df * np.log(cluster.size) if bic < cluster.bic(): self.__recursively_split([c1, c2]) else: self.__clusters.append(cluster) class Cluster: @classmethod def build(cls, X, cluster_model, index=None): if index is None: index = np.array(range(0, X.shape[0])) labels = range(0, len(np.unique(cluster_model.labels_))) return tuple(cls(X, index, cluster_model, label) for label in labels) # index: Xの各行におけるサンプルが元データの何行目のものかを示すベクトル def __init__(self, X, index, cluster_model, label): self.data = X[cluster_model.labels_ == label] self.index = index[cluster_model.labels_ == label] self.size = self.data.shape[0] self.df = self.data.shape[1] * (self.data.shape[1] + 3) / 2 center_ = cluster_model.cluster_centers_[label] self.center = X[center_, :] self.cov = np.cov(self.data.T) def log_likelihood(self): return sum([stats.multivariate_normal.logpdf(x, self.center, self.cov) for x in self.data]) def bic(self): return -2 * self.log_likelihood() + self.df * np.log(self.size) if __name__ == "__main__": colors = ['lightgreen', 'orange', 'lightblue', 'hotpink', 'yellow', 'lightmon'] markers = ['s', 'o', 'v', 'h', 'p', '+'] plt.figure(figsize=(10, 6)) n_clusters_list = np.arange(3, 6) for plot_num, n_clusters in enumerate(n_clusters_list): x_datas, labels = make_blobs(n_samples=200, n_features=2, centers=n_clusters, cluster_std=0.5, shuffle=True, random_state=0) # クラスタリングの実行 km = XMedoids(n_cluster=2, max_iter=300, n_init=10).fit(x_datas) predicted_values = km.labels_ medoids = km.cluster_centers_ unique_labels = sorted(np.unique(labels)) plt.subplot(len(n_clusters_list), 2, plot_num*2+1) for i, label in enumerate(unique_labels): plt.scatter(x_datas[labels==label, 0], x_datas[labels==label, 1], c=colors[i], marker=markers[i], s=15, label='cluster %s'%label) plt.title('cluster %d : true data'%n_clusters) plt.subplot(len(n_clusters_list), 2, plot_num*2+2) for i, label in enumerate(unique_labels): plt.scatter(x_datas[predicted_values==label, 0], x_datas[predicted_values==label, 1], c=colors[i], marker=markers[i], s=15, label='cluster %s'%label) plt.scatter(medoids[:, 0], medoids[:, 1], c='red', marker='*', s=100) plt.title('cluster %d : predicted data'%n_clusters) plt.tight_layout() plt.savefig(image_dir_path.joinpath('x_medoids.png').__str__()) plt.show()
class KMedoids(object): def __init__(self, n_cluster, max_iter=300, n_init=10): self.n_cluster = n_cluster self.max_iter = max_iter self.n_init = n_init def fit_predict(self, D): m, n = D.shape col_names = ['x_' + str(i + 1) for i in range(m)] best_results = None best_sse = np.Inf best_medoids = None for init_num in range(self.n_init): initial_medoids = np.random.choice(range(m), self.n_cluster, replace=False) tmp_D = D[:, initial_medoids] # 初期セントロイドの中で距離が最も近いセントロイドにクラスタリング labels = np.argmin(tmp_D, axis=1) # 各点に一意のIDが振ってあった方が分類したときに取り扱いやすいため # IDをもつようにするデータフレームを作っておく results = pd.DataFrame([range(m), labels]).T results.columns = ['id', 'label'] # 各点のIDと距離行列を結びつかせる # 距離行列の列に名前をつけて後々処理しやすいようにしている results = pd.concat([results, pd.DataFrame(D, columns=col_names)], axis=1) before_medoids = initial_medoids new_medoids = [] loop = 0 # medoidの群に変化があり、ループ回数がmax_iter未満なら続く while len(set(before_medoids).intersection(set(new_medoids))) != self.n_cluster and loop < self.max_iter: if loop > 0: before_medoids = new_medoids.copy() new_medoids = [] # 各クラスタにおいて、クラスタ内の他の点との距離の合計が最小の点を新しいクラスタとしている for i in range(self.n_cluster): tmp = results.ix[results['label'] == i, :].copy() # 各点において他の点との距離の合計を求めている tmp['distance'] = np.sum(tmp.ix[:, ['x_' + str(id + 1) for id in tmp['id']]].values, axis=1) tmp = tmp.reset_index(drop=True) # 上記で求めた距離が最初の点を新たなmedoidとしている new_medoids.append(tmp.loc[tmp['distance'].idxmin(), 'id']) new_medoids = sorted(new_medoids) tmp_D = D[:, new_medoids] # 新しいmedoidのなかで距離が最も最小なクラスタを新たに選択 clustaling_labels = np.argmin(tmp_D, axis=1) results['label'] = clustaling_labels loop += 1 # resultsに必要情報を追加 results = results.ix[:, ['id', 'label']] results['flag_medoid'] = 0 for medoid in new_medoids: results.ix[results['id'] == medoid, 'flag_medoid'] = 1 # 各medoidまでの距離 tmp_D = pd.DataFrame(tmp_D, columns=['medoid_distance'+str(i) for i in range(self.n_cluster)]) results = pd.concat([results, tmp_D], axis=1) sse = self.sse(distances=D, predicted_values=results['label'].values, medoids=new_medoids) if sse < best_sse: best_sse = sse best_results = results.copy() best_medoids = new_medoids.copy() self.labels_ = best_results['label'].values self.results = best_results self.cluster_centers_ = np.array(best_medoids) self.inertia_ = best_sse return self.labels_ def fit(self, D): m, n = D.shape col_names = ['x_' + str(i + 1) for i in range(m)] best_results = None best_sse = np.Inf best_medoids = None for init_num in range(self.n_init): initial_medoids = making_initial_medoids(D, n_cluster=self.n_cluster) tmp_D = D[:, initial_medoids] # 初期セントロイドの中で距離が最も近いセントロイドにクラスタリング labels = np.argmin(tmp_D, axis=1) results = pd.DataFrame([range(m), labels]).T results.columns = ['id', 'label'] results = pd.concat([results, pd.DataFrame(D, columns=col_names)], axis=1) before_medoids = initial_medoids new_medoids = [] loop = 0 while len(set(before_medoids).intersection(set(new_medoids))) != self.n_cluster and loop < self.max_iter: if loop > 0: before_medoids = new_medoids.copy() new_medoids = [] for i in range(self.n_cluster): tmp = results.ix[results['label'] == i, :].copy() tmp['distance'] = np.sum(tmp.ix[:, ['x_' + str(id + 1) for id in tmp['id']]].values, axis=1) tmp.reset_index(inplace=True) new_medoids.append(tmp.loc[tmp['distance'].idxmin(), 'id']) new_medoids = sorted(new_medoids) tmp_D = D[:, new_medoids] labels = np.argmin(tmp_D, axis=1) results['label'] = labels loop += 1 results = results.ix[:, ['id', 'label']] results['flag_medoid'] = 0 for medoid in new_medoids: results.ix[results['id'] == medoid, 'flag_medoid'] = 1 tmp_D = pd.DataFrame(tmp_D, columns=['label' + str(i) + '_distance' for i in range(self.n_cluster)]) results = pd.concat([results, tmp_D], axis=1) sse = self.sse(distances=D, predicted_values=results['label'].values, medoids=new_medoids) if sse < best_sse: best_sse = sse best_results = results.copy() best_medoids = new_medoids.copy() self.results = best_results self.cluster_centers_ = np.array(best_medoids) self.labels_ = self.results['label'].values return self # # クラス内誤差平方和を求める関数 # def sse(self, distances, predicted_values, medoids): unique_labels = sorted(np.unique(predicted_values)) sse = [] for label, medoid in zip(unique_labels, medoids): # 各クラスタの中心からの距離 distance = distances[medoid, predicted_values == label] distance_squared = distance * distance sse.extend(distance_squared.tolist()) return np.sum(sse)
参考文献
k-meansに関しては詳しことがすでに他の文献で書かれており、パッケージ化もされており、以下の本で詳しいことが書かれています。
*1:http://www.cs.cmu.edu/~dpelleg/download/xmeans.pdf
*2:https://media.accel-brain.com/jaccard-dice-simpson/
![[第3版]Python機械学習プログラミング 達人データサイエンティストによる理論と実践 impress top gearシリーズ [第3版]Python機械学習プログラミング 達人データサイエンティストによる理論と実践 impress top gearシリーズ](https://m.media-amazon.com/images/I/514u2pGsJNL._SL500_.jpg)